Performance

Here are a few comparisons between the data types provided by pgmp and the builtin PostgreSQL data types. A few observations:

• Of course mpz is not a substitute for decimal as it doesn’t store the non-integer part. So yes, we are comparing apples with pineapples, but decimal is the only currently available way to have arbitrary size numbers in PostgreSQL.

• We don’t claim the extra speed summing numbers with 1000 digits is something everybody needs, nor that applications doing a mix of math and other operations or under an I/O load will benefit of the same speedup.

• Those are “laptop comparisons”, not obtained with a tuned PostgreSQL installation nor on production-grade hardware. However they are probably fine enough to compare the difference in behaviour between the data types, and I expect the same performance ratio on different hardware with the same platform.

• All the results are obtained using the scripts available in the bench directory of the pmpz source code.

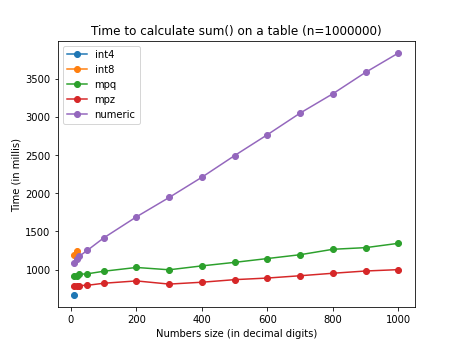
Just taking the sum of a table with 1M records, mpz is about 25% faster than numeric for small numbers; the difference increases with the size of the number up to about 75% for numbers with 1000 digits. int8 is probably slower than numeric because the numbers are cast to numeric before calculation. int4 is casted to int8 instead, so it still benefits of the speed of a native datatype. mpq behaves good as no canonicalization has to be performed.

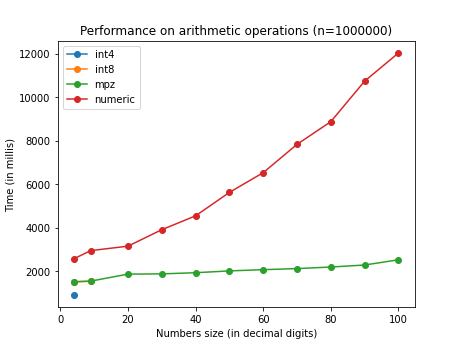
Performing a mix of operations the differences becomes more noticeable. This plot shows the time taken to calculate sum(a + b * c / d) on a 1M records table. mpz is about 45% faster for small numbers, up to 80% faster for numbers with 100 digits. int8 is not visible as perfectly overlapping mpz. mpq is not shown as out of scale (a test with smaller table reveals a quadratic behavior probably due to the canonicalization).

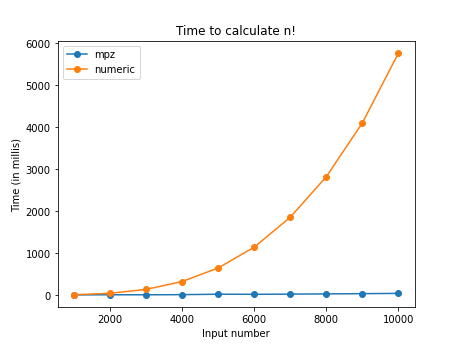
The difference in performance of multiplications is particularly evident: Here is a test calculating n! in a trivial way (performing the product of a sequence of numbers via a product aggregate function defined in SQL). The time taken to calculate 10000! via repeated mpz multiplications is about 40 ms.

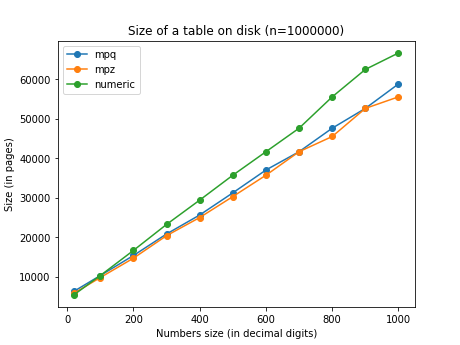
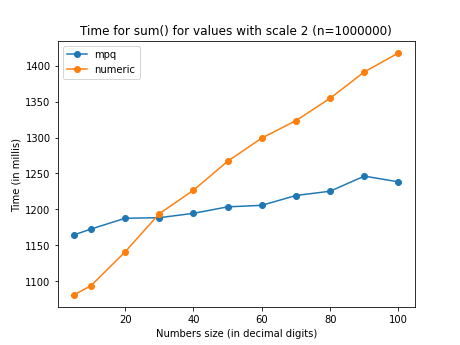
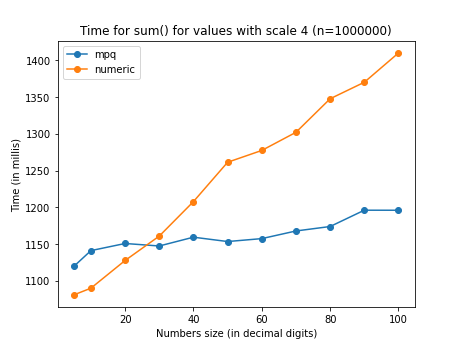
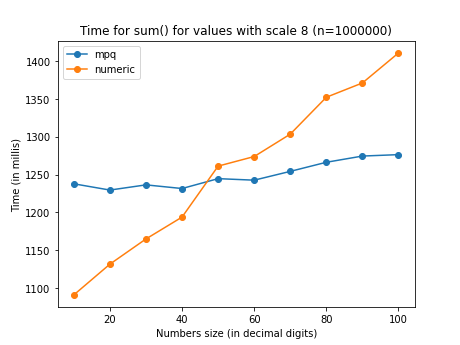
These comparisons show the perfomance with a sum of the same values stored in mpq and decimal. Because these rationals are representation of numbers with finite decimal expansion, the denominator doesn’t grow unbounded (as in sum(1/n) on a sequence of random numbers) but is capped by 10^scale. decimal is pretty stable in its performance for any scale but the time increases markedly with the precision (total number of digits). mpq grows way more slowly with the precision, but has a noticeable overhead increasing with the scale.

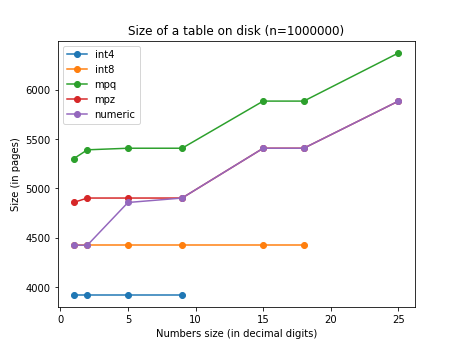
Here is a comparison of the size on disk of tables containing 1M records of different data types. The numbers are integers, so there is about a constant offset between mpz and mpq. The platform is 32 bit.